Выявление зависимости прибыли и рентабельности с помощью корреляционно-регресионного анализа

Проведем корреляционно-регрессионный анализ зависимости чистой прибыли и рентабельности собственного капитала.

Были использованы данные ОАО «Новгородхлеб» за 2004-2010 гг. по следующим показателям:

. рентабельность собственного капитала, % - результативный признак (у);

. чистая прибыль, тыс. руб. - факторный признак (х1);

. собственный капитал - факторный признак (х2).

Таблица 9

Расчетные данные

Были построены графики корреляционных полей зависимости рентабельности от чистой прибыли и рассчитаны показатели средней ошибки аппроксимации для того, чтобы определить оптимальную функцию:

. Линейная зависимость

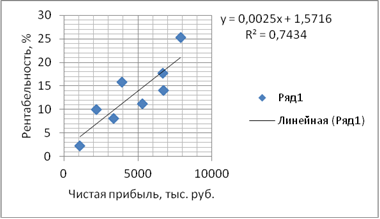
Рис. 2. Корреляционное поле зависимости рентабельности от чистой прибыли

Средняя ошибка аппроксимации находится по формуле:

= 30,47356

2. Полиномиальная зависимость

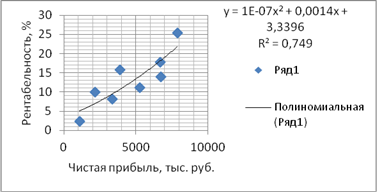
Рис. 3. Корреляционное поле зависимости рентабельности от чистой прибыли

= 32,24571

. Логарифмическая зависимость

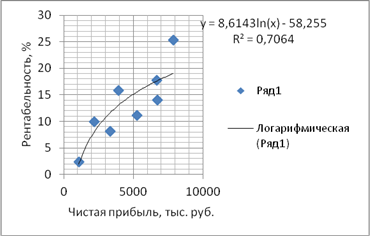
Рис. 4. Корреляционное поле зависимости рентабельности от чистой прибыли

=23,61889

. Степенная зависимость

статистический прогнозный прибыль рентабельность

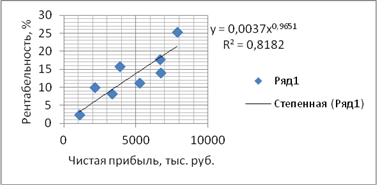
Рис.5. Корреляционное поле зависимости рентабельности от чистой прибыли

= 24,83090997

. Экспоненциальная зависимость

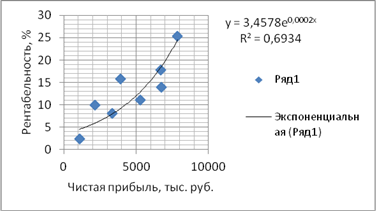
Рис. 6. Корреляционное поле зависимости рентабельности от чистой прибыли

= 34,37846

. Гиперболическая зависимость

0,12

100

Выбор оптимальной функции происходил на основе ошибки аппроксимации и коэффициента детерминации.

Не смотря на то, что наименьшая ошибка аппроксимации у логарифмической функции, коэффициент детерминации у неё не наибольший. Наибольший коэффициент детерминации у степенной функции, но у нее не наименьшая ошибка аппроксимации . Т.о., наиболее оптимальной является линейная функция, т.к. она обладает средними показателями.

На основе результатов регрессионного анализа (приложение А) сделаем следующие выводы:

Параметризованное уравнение у = 12,73071 - 0,00032х1 + 0,00263х2

Параметр а = 12,73071 - начальная точка отсчета, обусловленная влиянием других факторов, не учтенных в данной модели, параметр b1 = -0,00032 показывает, что если фактор х1 увеличить на единицу, то у уменьшится на 0,00032, знак минус при параметре свидетельствует о наличии обратной связи.

Другие материалы

Анализ деятельности турагентства ЗАО Спутник-Донецк
Туристическая отрасль приобретает все большее значение для развития экономики и социальной сферы в Украине, стремительно интегрируется в мировую туристическую индустрию. Приоритетное направление развития въездного и внутреннего туризма явля ...

Анализ финансового состояния предприятия, диагностика возможности банкротства и разработка рекомендаций и способов предотвращения кризисного состояния
В условиях рыночной экономики существенно возрос интерес участников экономического процесса к объективной и достоверной информации о финансовом состоянии, рентабельности и деловой активности предприятия. Все субъекты рыночных ...