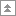Методика регрессионного анализа

Этот коэффициент изменяется от 0 до 1. Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние на и , то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:

(16)

Этот коэффициент изменяется от - 1 до +1.

Квадраты коэффициентов корреляции (2) - (4) называются коэффициентами (индексами) детерминации - соответственно парной, чистой (частной), множественной (совокупной):

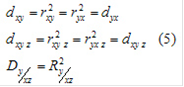(17)

Каждый из коэффициентов детерминации изменяется от 0 до 1 и оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной (y), обусловленную вариацией другой (других) - x и y. Многомерный случай наличия более трех переменных здесь не рассматривается.

Согласно разработкам английского статистика Р.Э. Фишера (1890-1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании -распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости и имеющейся степени свободы , где - число связей (факторных переменных). Для парного коэффициента имеем его среднеквадратическую ошибку и фактическое значение -критерия Стьюдента:

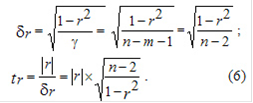(18)

Для чистого коэффициента корреляции при расчете его вместо (n-2) надо брать , т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.

Если tr

> tтабл., то коэффициент парной корреляции - общий или чистый является статистически значимым, а при tr

≤ tтабл. - незначимым.

Значимость коэффициента множественной корреляции R проверяется по F - критерию Фишера путем расчета его фактического значения

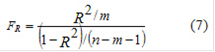(19)

При FR

> Fтабл. коэффициент R считается значимым с заданным уровнем значимости a и имеющихся степенях свободы и , а при Fr≤ Fтабл - незначимым.

В совокупностях большого объема n > 100 для оценки значимости всех коэффициентов Пирсона вместо критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).

Другие материалы

Первичный и вторичный рынок ценных бумаг
Российский рынок ценных бумаг, восстановленный заново в 90-е годы, относится к числу развивающихся. Создание современного рынка ценных бумаг в России становится одним из ключевых факторов оживления экономики страны. Государст ...

Анализ деятельности предприятия Конструкторское бюро химавтоматики
Производственная практика по дисциплине "Предпринимательская деятельность" в соответствии с государственным образовательным стандартом высшего профессионального образования по специальности "Профессиональное обучение (экономи ...