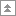Прогнозные значения
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (графа 6 таблицы 11). Используем эти оценки для расчета значений сезонной компоненты S (таблица 12). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты 
. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 12
Расчет значений сезонной компоненты в аддитивной модели
|
Показатели |
4 года |
№ гр. 4 года, i | |||
|
I |
II |
III |
IV | ||
|
1 |
-0,1 |
0,05 | |||
|
2 |
0,19 |
-1,24 |
-2,93 |
-0,27 | |
|
3 |
8,34 |
1,2 |
-6,38 |
3,17 | |
|
Итого за I квартал |
8,53 |
-0,04 |
-9,41 |
2,95 | |
|
Siср |
4,265 |
-0,02 |
-3,13667 |
0,983333 | |
|
Si |
3,74 |
-0,54 |
-3,66 |
0,46 | |
Для данной модели имеем:
,265 - 0,02 -3,13667 + 0,98 = 2,09
Определим корректирующий коэффициент: к = 2,09/4=0,522917
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
где 
,
Проверим условие равенства нулю суммы значений сезонной компоненты:
,74 - 0,54 - 3,66 + 0,46 = 0
Таким образом, получены следующие значения сезонной компоненты:
I 4 года: S1 = 3,74;
II4 года: S2 = -0,54;
III4 года:S3 = -3,66;
IV4 года:S 4= 0,46.
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины 
(графа 4 таблицы 13). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Таблица 13
Расчет выровненных значений T и ошибок E в аддитивной модели
|
t |
Yt |
Si |
T+E=Yt-Si |
T |
T+S |
E=Yt-(T+S) |
EІ |
(Yt-Ytср)І |
|
1 |
7 |
4,27 |
2,73 |
8,356 |
12,626 |
-5,63 |
31,65 |
49,00 |
|
2 |
7,9 |
-0,02 |
7,92 |
8,6432 |
8,6232 |
-0,72 |
0,52 |
62,41 |
|
3 |
8 |
-3,14 |
11,14 |
8,9304 |
5,7904 |
2,21 |
4,88 |
64,00 |
|
4 |
8,5 |
0,98 |
7,52 |
9,2176 |
10,1976 |
-1,70 |
2,88 |
72,25 |
|
5 |
9 |
4,27 |
4,73 |
9,5048 |
13,7748 |
-4,77 |
22,80 |
81,00 |
|
6 |
8,73 |
-0,02 |
8,75 |
9,792 |
9,772 |
-1,04 |
1,09 |
76,21 |
|
7 |
10 |
-3,14 |
13,14 |
10,0792 |
6,9392 |
3,06 |
9,37 |
100,00 |
|
8 |
15,82 |
0,98 |
14,84 |
10,3664 |
11,3464 |
4,47 |
20,01 |
250,27 |
|
9 |
25,33 |
4,27 |
21,06 |
10,6536 |
14,9236 |
10,41 |
108,29 |
641,61 |
|
10 |
17,73 |
-0,02 |
17,75 |
10,9408 |
10,9208 |
6,81 |
46,37 |
314,35 |
|
11 |
8,15 |
-3,14 |
11,29 |
11,228 |
8,088 |
0,06 |
0,00 |
66,42 |
|
12 |
14 |
0,98 |
13,02 |
11,5152 |
12,4952 |
1,50 |
2,26 |
196,00 |
|
13 |
11,14 |
4,27 |
6,87 |
11,8024 |
16,0724 |
-4,93 |
24,33 |
124,10 |
|
14 |
2,34 |
-0,02 |
2,36 |
12,0896 |
12,0696 |
-9,73 |
94,67 |
5,48 |
|
Итого |
153,64 |
- |
- |
131,0296 |
- |
- |
274,46 |
2097,63 |
|
Среднее |
10,97 |
Другие материалы
Пути увеличения объёма производства и реализации продукции
По мере становления России на рыночный путь развития экономики повышается
роль таких показателей, как объем производства и реализации продукции
предприятия. Именно эти показатели являются решающим фактором формирования
прибыл ...
Анализ и экономическая оценка эффективности использования основных фондов предприятия ООО Гостиный двор-2001
Основные фонды представляют собой объекты имущества организации, используемые в качестве средств труда при производстве продукции, выполнении работ и оказании услуг, либо для управления организацией в течение периода, превышающего 12 месяце ...
Главное меню
