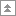Прогнозные значения
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (графа 6 таблицы). Используем эти оценки для расчета значений сезонной компоненты S (таблица). Для этого найдем средние за каждый год оценки сезонной компоненты 
. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем годам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4 (четыре года).
Таблица 15
Расчет сезонной компоненты в мультипликативной модели
|
Показатели |
4 года |
№ гр. 4 года, i | |||
|
I |
II |
III |
IV | ||
|
1 |
- |
- |
0,99 |
1,01 | |
|
2 |
1,02 |
0,88 |
0,77 |
0,98 | |
|
3 |
1,49 |
1,07 |
0,56 |
1,29 | |
|
Итого за I квартал |
2,51 |
1,95 |
2,32 |
3,28 | |
|
Siср |
1,255 |
0,975 |
0,77 |
1,09 | |
|
Si |
1,23 |
0,95 |
0,76 |
1,07 | |
Имеем:
,255 + 0,975 +2,32 +3,28 = 4,10
Определим корректирующий коэффициент: 
.
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент k.
где 
,
Проверим условие равенства 4 суммы значений сезонной компоненты:
,23 +0,95 +0,76+1,07 = 4
Получим следующие значения сезонной компоненты:
I4 года:
;
II4 года: 
III4 года: 
;
IV4 года: 
Занесем полученные значения в таблицу для соответствующих кварталов каждого года (графа 3).
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины 
(графа 4 таблицы 16), которые содержат только тенденцию и случайную компоненту.
Таблица 16
Расчет выровненных значений Τ и ошибок Ε в мультипликативной модели
|
t |
Yt |
Si |
T*E=Yt/Si |
T |
T*S |
E=Y/(T*S) |
EІ |
(Yt-(T*S))^2 |
(Yt-Ytср)І |
|
1 |
7 |
1,23 |
5,69 |
9,376 |
11,53248 |
0,61 |
0,37 |
20,54 |
49,00 |
|
2 |
7,9 |
0,95 |
8,32 |
9,5985 |
9,118575 |
0,87 |
0,75 |
1,48 |
62,41 |
|
3 |
8 |
0,76 |
10,53 |
9,821 |
7,46396 |
1,07 |
1,15 |
0,29 |
64,00 |
|
4 |
8,5 |
1,07 |
7,94 |
10,0435 |
10,74655 |
0,79 |
0,63 |
5,05 |
72,25 |
|
5 |
9 |
1,23 |
7,32 |
10,266 |
12,62718 |
0,71 |
0,51 |
13,16 |
81,00 |
|
6 |
8,73 |
0,95 |
9,19 |
10,4885 |
9,964075 |
0,88 |
0,77 |
1,52 |
76,21 |
|
7 |
10 |
0,76 |
13,16 |
10,711 |
8,14036 |
1,23 |
1,51 |
3,46 |
100,00 |
|
8 |
15,82 |
1,07 |
14,79 |
10,9335 |
11,69885 |
1,35 |
1,83 |
16,98 |
250,27 |
|
9 |
25,33 |
1,23 |
20,59 |
11,156 |
13,72188 |
1,85 |
3,41 |
134,75 |
641,61 |
|
10 |
17,73 |
0,95 |
18,66 |
11,3785 |
10,80958 |
1,64 |
2,69 |
47,89 |
314,35 |
|
11 |
8,15 |
0,76 |
10,72 |
11,601 |
8,81676 |
0,92 |
0,85 |
0,44 |
66,42 |
|
12 |
14 |
1,07 |
13,08 |
11,8235 |
12,65115 |
1,11 |
1,22 |
1,82 |
196,00 |
|
13 |
11,14 |
1,23 |
9,06 |
12,046 |
14,81658 |
0,75 |
0,57 |
13,52 |
124,10 |
|
14 |
2,34 |
0,95 |
2,46 |
12,2685 |
11,65508 |
0,20 |
0,04 |
86,77 |
5,48 |
|
Итого |
153,64 |
- |
- |
139,243 |
- |
- |
16,25 |
347,68 |
2097,63 |
|
Среднее |
10,97 |
Другие материалы
Оценка результатов хозяйственно-финансовой деятельности ОАО Роснефть
Сегодня,
когда наша страна интенсивно строит новые экономические отношения, укрепляет
свои позиции в мире, интегрируется в международный рынок, отечественный
топливно-энергетический комплекс остается важнейшей, основопола ...
Анализ показателей прибыли и рентабельности ОАО Новгородхлеб
В рыночной экономике успешность ведения бизнеса определяется наличием ряда ключевых условий. Во-первых, это четкое определение сферы деятельности, то есть устойчивое занятие собственной ниши на рынке товаров и услуг. Во-вторых, это формиров ...
Главное меню
